二叉树递归的要点

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后序遍历。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置 --- 第1次访问该节点
    traverse(root.left);
    // 中序位置 --- 第2次访问该节点
    traverse(root.right);
    // 后序位置 --- 第3次访问该节点
}

所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候。

1
2
3
4
5
6
7
8
9


/* 递归遍历单链表，倒序打印链表元素 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    traverse(head.next);
    // 后序位置
    print(head.val);
}

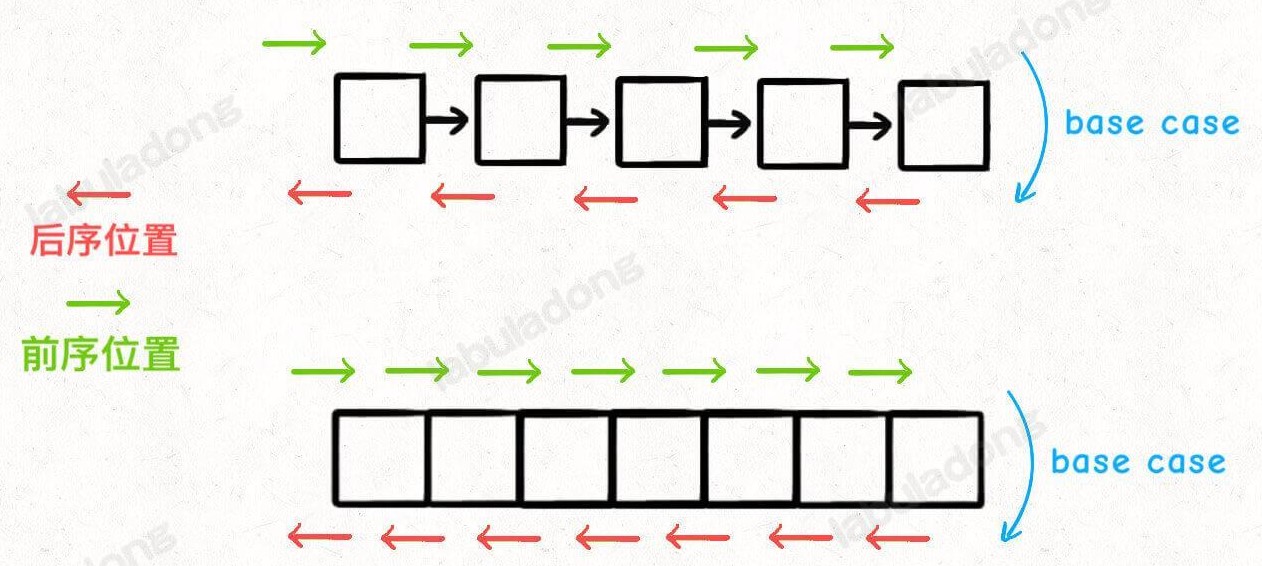
前序位置的代码在刚刚进入一个二叉树节点的时候执行；

后序位置的代码在将要离开一个二叉树节点的时候执行；

中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。中序遍历是二叉树特有的。

二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，代码模板中不需要返回值；第二类是通过分解问题计算出答案，子问题返回值视题目而定，一般有返回值。这两类思路分别对应着「回溯算法核心框架」和「动态规划核心框架」。

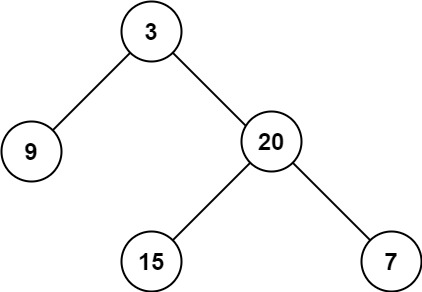
以计算二叉树最大深度为例：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


/*遍历法*/
int result = 0; //记录最大深度
int depth = 0; //记录当前深度
void traverse(TreeNode root) {
    if (head == null) {
        return;
    }
    
    depth++;// 第一次访问节点
    if (root.left == null && root.right == null) {
        result = Math,max(result, depth); //叶子节点更新距离
    }
    traverse(root.left);
    // 判断逻辑写在这里也行 --- 本质上深度被正确标定
    traverse(root.right);
    // 判断逻辑写在这里也行 --- 本质上深度被正确标定
    depth--;// 最后一次访问节点，离开
}

1
2
3
4
5
6
7
8
9


/*分解问题法*/ --- 左子树的最大深度 和 右子树的最大深度 中最大的 + 自己
public int maxDepth(TreeNode root) { //maxDepth的定义为：输入一个节点，返回最大深度
    if (root == null) {
        return 0;
    }
    int leftdepth = maxDepth(root.left);
    int rightdepth = maxDepth(root.right);
    return Math.max(leftdepth, rightdepth) + 1;
}

对于分解问题法，个人认为不要陷入递归中思考，从逻辑上考虑就可以。

再来一个收集遍历结果的例子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


/*遍历法*/
List<Integer> res = new LinkedList<>();

List<Integer> preorderTraverse(TreeNode root) {
    traverse(root);
    return res;
}

void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置
    res.add(root.val);
    traverse(root.left);
    traverse(root.right);
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


/*分解问题法*/ --- 输入一棵二叉树的根节点，返回这棵树的前序遍历结果
List<Integer> preorderTraverse(TreeNode root) {
    List<Integer> res = new LinkedList<>();
    if (root == null) {
        return res;
    }
    // 前序遍历的结果，root.val 在第一个
    res.add(root.val);
    // 利用函数定义，后面接着左子树的前序遍历结果
    res.addAll(preorderTraverse(root.left));
    // 利用函数定义，最后接着右子树的前序遍历结果
    res.addAll(preorderTraverse(root.right));
    return res;
}

后序位置的特殊之处

前序位置的代码执行是自顶向下的，而后序位置的代码执行是自底向上的。

前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// 打印第几层
void traverse(TreeNode root, int level) {
    if (root == null) {
        return;
    }
    // 前序位置
    printf("节点 %s 在第 %d 层", root, level);
    traverse(root.left, level + 1);
    traverse(root.right, level + 1);
}

// 这样调用
traverse(root, 1);

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


// 打印左右子树几个节点
// 定义：输入一棵二叉树，返回这棵二叉树的节点总数
int count(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftCount = count(root.left);
    int rightCount = count(root.right);
    // 后序位置 --- 只有离开时才能拿到左右子树的信息
    printf("节点 %s 的左子树有 %d 个节点，右子树有 %d 个节点",
            root, leftCount, rightCount);

    return leftCount + rightCount + 1;
}

一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

算法拾遗-二叉树递归问题

二叉树递归的要点

后序位置的特殊之处